
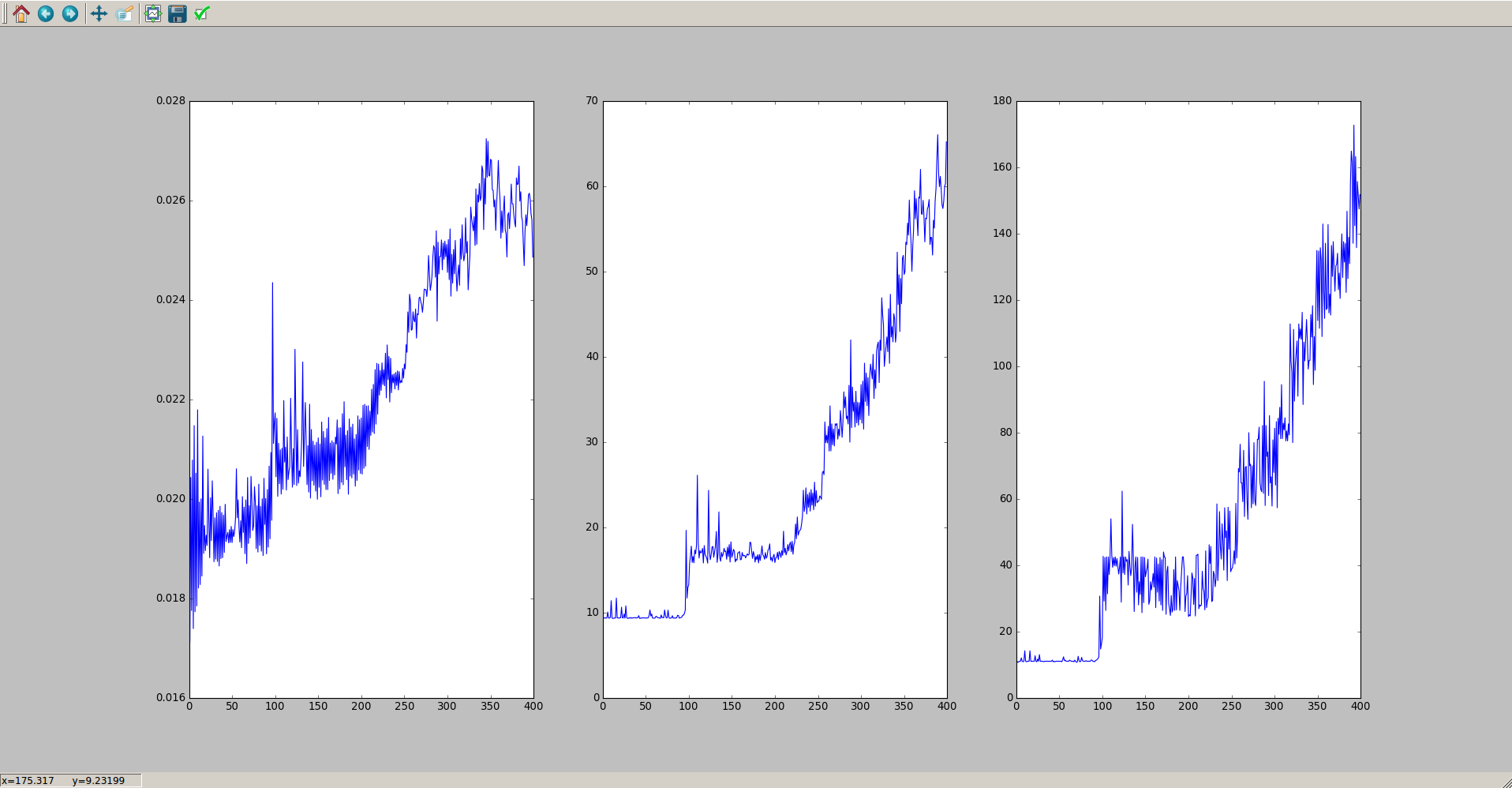
This property motivates the Augmented Dickey-Fuller Test, which we will describe below. In a discrete setting the equation states that the change of the price series in the next time period is proportional to the difference between the mean price and the current price, with the addition of Gaussian noise. Where $\theta$ is the rate of reversion to the mean, $\mu$ is the mean value of the process, $\sigma$ is the variance of the process and $W_t$ is a Wiener Process or Brownian Motion. Testing for Mean ReversionĪ continuous mean-reverting time series can be represented by an Ornstein-Uhlenbeck stochastic differential equation:ĭ x_t = \theta (\mu - x_t) dt + \sigma dW_t
#Long run average sequential testing brownian motion how to#
In particular, we will study the concept of stationarity and how to test for it. In this article we are going to outline the statistical tests necessary to identify mean reversion. The mean-reverting property of a time series can be exploited in order to produce profitable trading strategies.
This is in contrast to a random walk (Brownian motion), which has no "memory" of where it has been at each particular instance of time. Mathematically, such a (continuous) time series is referred to as an Ornstein-Uhlenbeck process. This process refers to a time series that displays a tendency to revert to its historical mean value. One of the key trading concepts in the quantitative toolbox is that of mean reversion. It is now time to turn our attention towards forming actual trading strategies and how to implement them.

So far on QuantStart we have discussed algorithmic trading strategy identification, successful backtesting, securities master databases and how to construct a software research environment. The code below is a modification of that which used to be found on his website, which later became. Tom Starke for providing the inspiration for this article series.


 0 kommentar(er)
0 kommentar(er)
